česky
previous main page content next

Adaptive Huffman coding - Vitter's algorithm (Λ)

Main features

Time and space complexities

Time complexity of algorithm: O(n*log|Σ|)
Space complexity of algorithm: O(|Σ|)

History

Conventional Huffman coding was improved by Faller, Gallager and Knuth to faster algorithm, named by the first letters of their names FGK. Next improvement was introduced by Jeffrey Scott Vitter in 1987. It is similar to FGK algorithm, but it is using another way of tree updating.

Description

Basic principles of Λ algorithm are the same as in FGK algorithm. Sender and the receiver maintain equivalent dynamically varying Huffman trees, which contains all already coded characters as its leaves. Inner nodes of this tree are nodes with sum of counts of nodes in its subtree. There is also one special node in the tree - node ZERO. Code of node ZERO is used as an escape sequence.

When some new character, which is already in the tree, is received , the code of its node is written to output and the tree has to be updated. If it is the first occurrence of this character, the code of node ZERO and the character (in some format) are written to output. Then the node ZERO is replaced with a new inner node. Children of this node are ZERO node and a new node containing the character. The update is started from the last coded character (or newly added node character). First the block which precedes this node has to be determined. Block of nodes is the group of nodes with the same values and with the same type - it means they are all inner nodes or leaves. If it is necessary to slide (see pseudocode), node will move in front of the selected block (left rotation) and the process of updating is repeated at a higher level.

The difference between FGK algorithm and Vitter's algorithm can be seen on the pictures next. Character sequence abacabdabaceabacabdf was coded. Both algorithms created (in different ways) the same trees. If the next character is G, algorithms will give different results. Vitter's tree is more balanced than FGK tree.

FGK:
FGK 		Vitter:
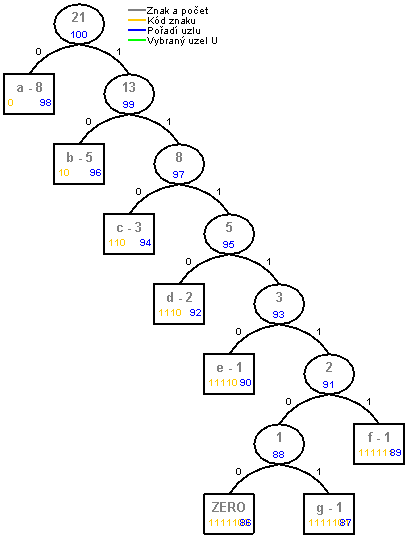
Vitter

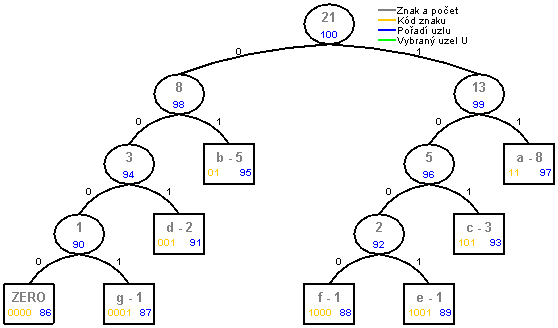
Pseudo-code


 1:  begin
 2:     Initialize 
 3:     readSymbol(X)
 4:     while (X!=EOF) do 
 5:      begin
 6:        if (first_read_of(X)) then 
 7:         begin
 8:           output(code of ZERO) 
 9:           output(code of node X)
10:           create new node U with next node ZERO and new node X
11:           update_tree(U);
12:         end
13:        else
14:         begin
15:           output(code of node X)
16:           update_tree(node X)
17:         end
18:        readSymbol(X)
19:      end
20:  end 
21:    
22:  procedure update_tree(U)
23:  begin
24:     while (U!=root) do 
25:      begin
26:        b := block of nodes preceding node U
27:        if ((U is leaf) and (b is block of inner nodes) and (value U == value b))
28:          or ((U is inner node) and (b is block of leaves) and (value U == value b - 1)) then
29:         begin
30:           slide U in front of block b
31:           increment value of U
32:           if (U is leaf) then 
33:              U := parent(U)
34:           else 
35:              U := parent (U before slide)
36:         end
37:        else
38:         begin
39:           increment value U
40:           U := parent(U)
41:         end
42:      end
43:     increment value U
44:  end

References and literature

  1. Official site of J. S. Vitter
  2. J. S. Vitter: Design and analysis of dynamic Huffman codes. Journal of ACM 34, 4 (Oct. 1987), 825-845.
  3. J. S. Vitter: Algorithm 673 Dynamic Huffman Coding. ACM Transactions on Mathematical Software, 15(2), June 1989, 158-167 (1989).
  4. Adaptive Huffman coding. Wikipedia, the free encyclopedia.
  5. Adaptive Huffman coding description - FGK and Vitter

Example